资料
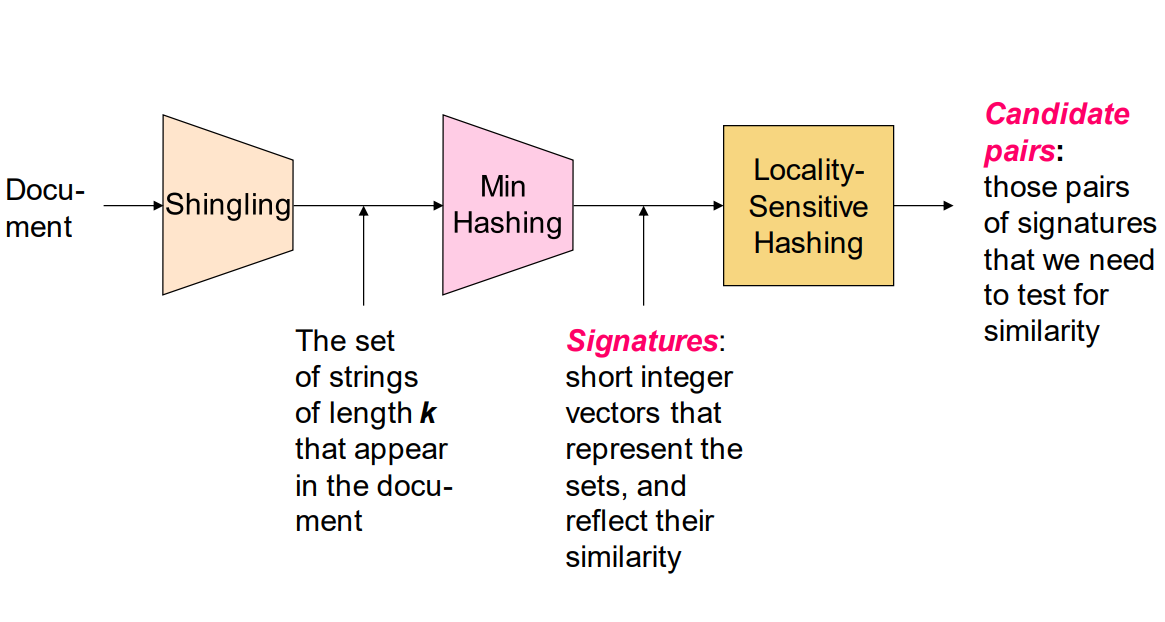
Shingling
Shingling(也称为k-gram)是一种将文本或序列数据转换为具有固定大小的片段的技术。
Shingling的基本思想是将文本或序列数据分割成连续的、非重叠的片段,每个片段称为一个shingle。这些shingle可以是字符级别的、单词级别的或其他更大的语言单元。然后,通过表示这些shingle的集合或哈希值,来描述原始文本或序列数据的特征。
具体来说,Shingling过程包括以下步骤:
- 将文本或序列数据分割成固定长度的片段,例如,将文本分割成长度为k的连续字符或单词。
- 对于每个片段,生成一个唯一的标识符(例如,哈希值)来表示该片段。
- 将所有片段的标识符组合成一个集合或向量,表示原始文本或序列数据的shingle特征。
Document 𝑫𝒊 is represented by a set of its k-shingles 𝑪𝒊 = 𝑺(𝑫𝒊)
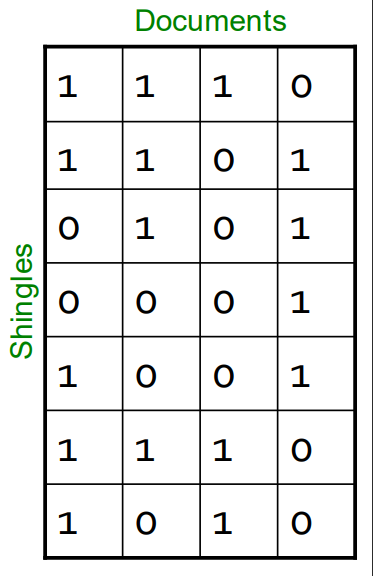
Rows = elements (shingles)
Columns = sets (documents)
通常会生成一个稀疏矩阵。
minhash
哈希签名
原始集合按列组成的矩阵,将这个矩阵按行打乱排序P次,在每一次打乱之后,找出每个集合(即矩阵的列向量)的第一个值为1的行索引,并将这个索引分别填充进一个新的集合中(每个原始集合拥有各自的一个新的集合),这个新的集合就是原始集合的哈希签名。
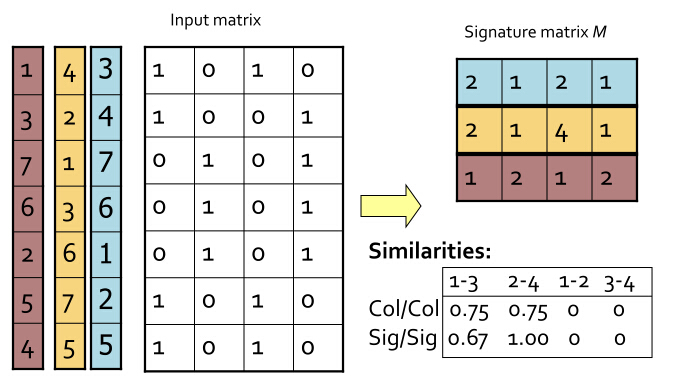
在经过随机行打乱后,两个集合的最小哈希值相等的概率等于这两个集合的Jaccard相似度。
在现实中排列一个很大的行索引也是很慢的,所以一般用随机的哈希函数来替代排列。
缺点
当矩阵很大,计算多个哈希函数的代价是相当昂贵的
改进
对于每个集合,使用这个单一的哈希函数选出其中的多个值,而不是每个哈希函数选择一个值。
前面我们定义过 hmin(S)为集合S中具有最小哈希值的一个元素,那么我们也可以定义hmink(S)为集合S中具有最小哈希值的K个元素。这样一来,我们就只需要对每个集合求一次哈希,然后取最小的K个元素。计算两个集合A、B的相似度,就是集合A中最小的K个元素与集合B中最小的K个元素的交集个数与并集个数的比例。
band
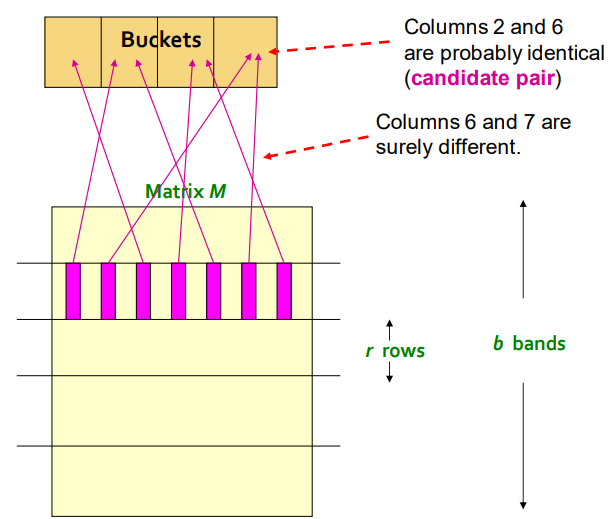
Band是一种用于将MinHash签名划分成多个块的技术。通过将MinHash签名分组到不同的Band中,可以更精确地定位相似集合,同时减少计算量。
背景
MinHash算法使用Band技术的目的是减少相似性比较的计算开销,并提高算法的效率和可扩展性。通过将MinHash签名划分成多个Band,可以在比较相似集合时只需要比较相同Band中的桶,而不必比较所有的MinHash值。
基本原理
-
将MinHash签名分成多个Band。每个Band由多个行组成,每行包含一个MinHash值。
-
对于每个Band,计算其哈希值。将相同Band哈希值的MinHash值归为一组。
-
每个Band生成一个带有哈希值的桶。每个桶中包含该Band中所有MinHash值的标识符。
通过比较相同Band的桶,可以确定相似集合的候选对。
Band的数量和每个Band的行数是根据具体应用和数据集进行选择的。较小的Band数量和较大的行数可以提供更高的召回率(找到更多的相似集合),但会增加计算开销。相反,较大的Band数量和较小的行数可以提供更高的准确率(减少误报),但可能会减少召回率。
分析
上面得到向量可以分为b段(桶),每个段有r个行,假设两个点的Jaccard相似度为s,根据 minHash的值相等的概率等于Jaccard相似度 这个定理,若两个点在某个段完全相同,则认为这两个点为相似对。分析如下:
- 两个点在一个段中,完全一样的概率为
s^r - 两个点在一个段中,不完全一样的概率为
1-s^r - 两个点在所有段中,不完全一样的概率为
(1-s^r)^b - 两个点至少有一个段相同的概率为
1-(1-s^r)^b